5数要約(5 number summary)
5数要約とは、データの分布状況を5つの量にまとめたものです。5つの量とは、小さい順に最小値、下側四分位置、中央値、上側四分位です。英語では、the sample minimum (smallest observation)、the lower quartile or first quartile、the median (middle value)、the upper quartile or third quartile、the sample maximum (largest observation)の5つです。
中央値は全データのmedianです。下側四分位置は最小値と中央値間のmedian、同じく上側四分位は最大値と中央値間のmedianです。
箱ひげ図
下側四分位置と上側四分位置の間を箱で表現しまます。
上側四分位から下側四分位置を引いた値を、IQR(interquartile range) とします。下側四分位置からIRQの1.5倍を引いたものを下側内堀、上側四分位置にIRQの1.5倍を足したものを上側内堀とします。下側内堀と上側内堀の中の最小値と最大値を、箱ひげ図のひげとして表現します。
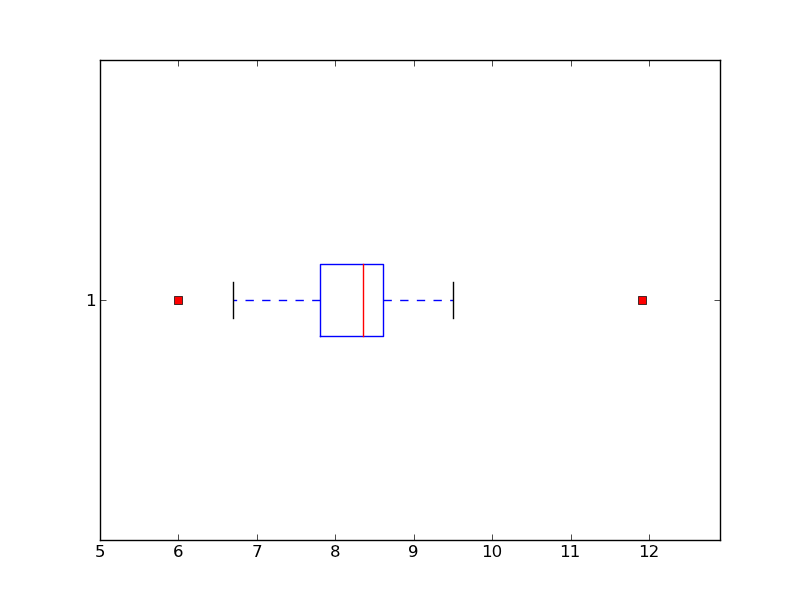
pyplotで箱ひげ図を書く。
pyplotを使うと箱ひげ図を簡単に書くことができます。元データは、例題で学ぶ統計的方法 15ページから。
# python3 __author__ = 'natu' from pylab import * data = [7.4, 7.7, 8,6, 8.1, 8.6, 8.3, 8.3, 7.3, 8.7, 8.5, 7.3, 8.4, 8.5, 8.6, 8.6, 8.8, 7.7, 8.6, 8.2, 11.9, 7.6, 8.3, 7.8, 8.8, 9.4, 8.6, 8.6, 7.9, 8.5, 8.2, 8.7, 8.8, 8.2, 8.4, 7.9, 8.7, 7.5, 8.1, 6.7, 8.6, 7.6, 8.6, 9.5, 7.6, 7.8, 8.7, 8.5] # xlimで使う最大値と最小値を求める。 data.sort() min = data[0] max = data[-1] figure() boxplot(data,0,'rs',0) xlim(min-1.0,max+1.0) savefig('boxplot.png') show()